Two Class Quadratic Classifier

It is a good exercise to analyze how to Bayes Theorem to estimate the posterior probability for each class in a two class scenario.

The decision boundary can be identified as:

$$f(\mathbf{x})=\log \frac{p(y_1|\mathbf{x})}{p(y_2|\mathbf{x})}=\log 1$$ $$f(\mathbf{x})=\log (y_1|\mathbf{x})-\log p(y_2|\mathbf{x})=0$$

Replacing the class conditional probabilities with the gaussian distribution, we can derive that:

$$p(y|\mathbf{x})=\frac{p(\mathbf{x}|y)p(y)}{p(\mathbf{x})}$$ $$p(\mathbf{x}|y)=\frac{1}{(\sqrt{2\pi {)}^{p}det({\Sigma }_y)}}exp(-\frac{1}{2}(x-{\mu }_y){\Sigma }_y^{-1}(x-{\mu }_y))$$

Deriving the logarithm of the class posteriors:

$$\log (p(y|\mathbf{x})=\frac{-p}{2}2\pi -\frac{1}{2}det({\Sigma }_y)-\frac{1}{2}(x-{\mu }_y){\Sigma }_y^{-1}(x-{\mu }_y)+\log p(y)-\log p(\mathbf{x})$$

Since $p(\mathbf{x})$ is independent of the class, it can be dropped, leaving us with:

$$g_i(\mathbf{x})=\frac{-p}{2}2\pi -\frac{1}{2}det({\Sigma }_{y_i})-\frac{1}{2}(x-{\mu }_{y_i}){\Sigma }_{y_i}^{-1}(x-{\mu }_{y_i})+\log p(y_i)$$

Therefore, the classifier becomes $g_i(\mathbf{x})>g_j(\mathbf{x})$. And the decision boundary becomes $f(\mathbf{x})=g_2(\mathbf{x})-g_1(\mathbf{x})=0$.

The function $f(\mathbf{x})$ can be written in the general form:

$$f(\mathbf{x})={\mathbf{x}}^T\mathbf{Wx}+{\mathbf{w}}^T\mathbf{x}+w_0$$

where

$$\mathbf{W}=\frac{1}{2}({\Sigma }_2^{-1}-{\Sigma }_1^{-1})$$ $$\mathbf{W}={\mu }_1^T{\Sigma }_1^{-1}-{\mu }_2^T{\Sigma }_2^{-1}$$ $$w_0=-\frac{1}{2}\log \det {\Sigma }_1-\frac{1}{2}{\mu }_1^T{\Sigma }_1^{-1}{\mu }_1+\log p(y_1)+\frac{1}{2}\log \det {\Sigma }_2+\frac{1}{2}{\mu }_2^T{\Sigma }_2^{-1}{\mu }_2-\log p(y_2)$$

This leaves us with a quadratic decision boundary:

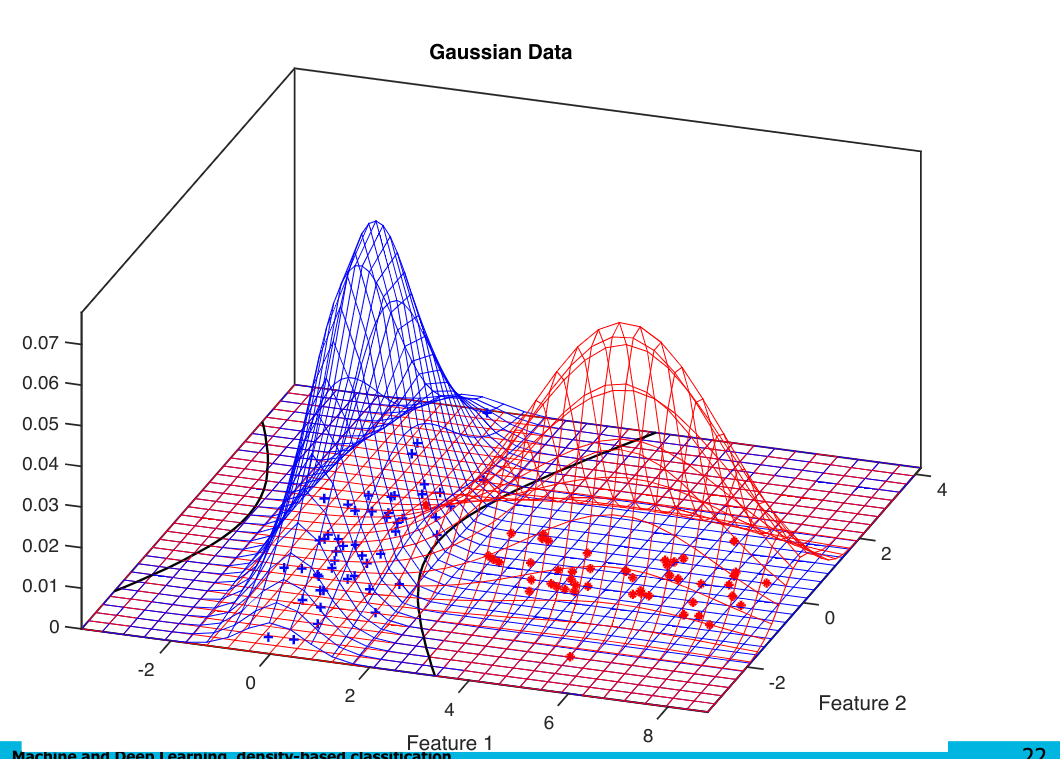
What if the covariance matrix is non invertible?

In the case that one of the variances of a feature’s variance is 0: we can not write an inverse matrix for $\Sigma$. So, instead we estimate a single covariance matrix for the entire dataset by averaging over the covariance matrices for all classes:

$$\hat{}=\frac{1}{N}{\Sigma }_{i=1}^N{\Sigma }_i$$

Since we share a single covariance matrix across all classes, the matrix $\mathbf{W}$ becomes 0, turning $f(\mathbf{x})={\mathbf{w}}^T\mathbf{x}+w_0$, and making our decision boundary linear.

No covariance matrix 🥺

If you are unable to even estimate a single covariance matrix, one can simply assume that the variance of each feature is the same and are independent from each other. This results in a covariance matrix in the form of: $\hat{\Sigma }={\sigma }^{2}I$